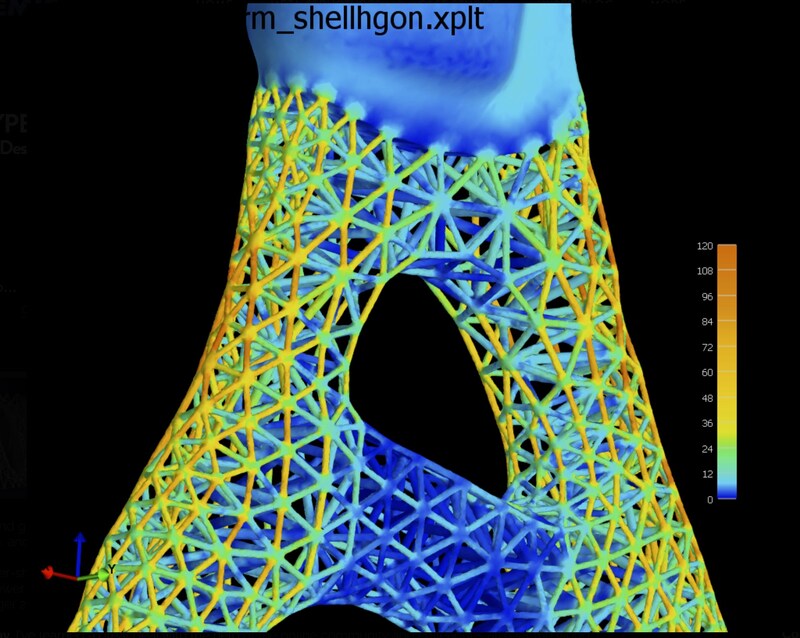
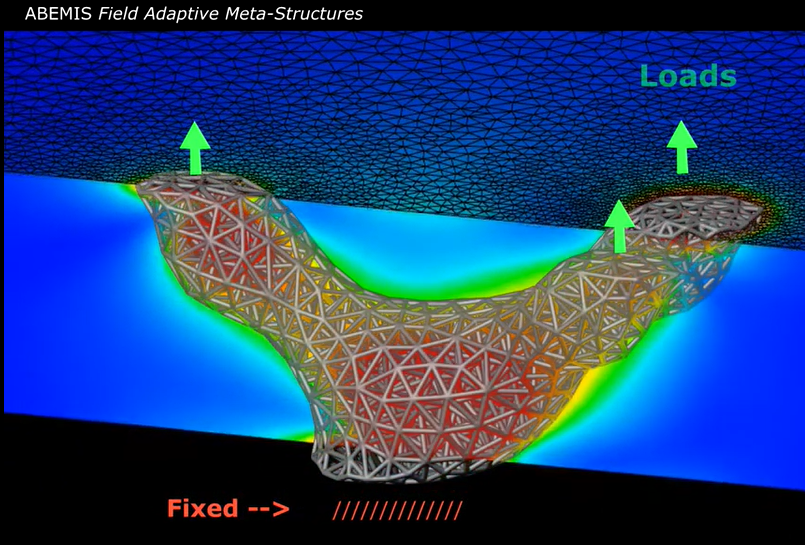
 In Part 1 we showed that Meta-topology optimization can be used to generate completely novel, ultra-light structures. In addition to surface optimization, meta-structures can also meta-adapt to functional stresses and loads. Here I'll describe a very simple example of stress optimization using combined surface and meta-topology approach. The basic idea is that the exterior surface shape is determined (and controlled) by regional stress, and the corresponding HGon meta-structure is generated and optimized from both the regional and meta-stress calculation. Some background info: There is a wealth of information about topological surface optimization (TSO) on the web. Many companies such as Altair, PTC, Autodesk, and nTopology are providing software tools. nTopology's "platform" software has quite an amazing GUI interface and tools that include lattice-type structures. Here is the Wikipedia and some links to interesting intros and articles: - This Altair report has a great basic introduction (PDF) - Book chapter by Akyut Kentli: Link - Master's Thesis by Robin Larsson (Link) has a good intro and method overview - PhD Thesis by Philip Browne (Link) goes into detail for elastic structures, many references - Deep Learning applied to Topo-optimization: Link Note: this is a new research focus for us at ABĒMIS; with very exciting potential for 'intelligent' meta-structure optimization. Please email me me for more info and progress in this area. - A bunch more examples and info here: Link If any of these links don't work, please comment or email me (nothing shared, no lists). In this article/post we start with a very simple example "brick" that has just two offset connections. The lower larger connection is fixed (see Fig. above), and the upper smaller connection is loaded in the Z-direction. The same procedure also applies to more (or essentially, any) complex components and loading conditions (we'll see some more complex examples in Part 3). Meta-topology optimization has four basic steps: Step 1 - similar to standard topology optimization, the overall component stresses are calculated using FEA, and isosurface(s) are computed for optimized outer shape. We do the optimization calculations in a combination of Python and C++. Step 2 - the HGon meta-structure is generated from the isosurface, with nominal meta-strut thickness (set to 1mm radius, or whatever is favorable). We call this the 'base' HGon meta-structure. Step 3 - the stresses carried by the meta-struts (0nly) are computed. The meta-stress field is interpolated to a high resolution volumetric object (typically 8x of the minimum meta-strut thickness). Step 4 - the meta-struts and joints are 'thickened' or 'thinned' according to a combination of regional and local-meta stress computed in step 3. This process is repeated until desired and/or computed criteria are met, such as minimized mass, maximized surface area, or maximized fatigue strength among many other possibilities. Objective functions can be simple or complex combining many strategies, fields, and loading. The result (below) for this simple Z-axis loading shows meta-struts "thickened" where the stress is highest, and "thinned" at low stress. HGon overall stiffness in this example is thus increased by >135%, without (in this case) increasing the overall mass! Essentially, the meta-topology and surface is adapted to reduce stresses: The resulting meta-optimized HGon has thickened struts in regions of elevated stress. Of course, this procedure can be extended from this very simple example to much more complex shapes and boundary conditions. A great advantage of HGon-type metastructures is the ability to conform to extremely complex shapes. Factors of safety fields can also be included to ensure regional thicknesses maintain overload capabilities. Multiple fields, instead of just von Mises stress can be combined. For example, the optimization can be driven by tension and shear stress in the meta-FEA, and von Mises stress in the regional FEA, or any other combination. In fact, pretty much any computable FEA fields can be used: heat transfer, fluid flow, electrostatic/dynamic, and vibrations modal/dynamic, just naming a few. Vibration damping (and excitation) is another primary focus of our current work. Below is an example of the same 'brick', but this time with 3 upper connections instead of just one. This produces a more complex HGon meta-structure. Again, we are using only Z-axis load. HGon meta-optimized structures for a more complex example with three loaded connections. Preceding was just the most brief explanation and simple examples of HGon meta-optimization. The possibilities for advanced generative design with new HGon conforming meta-structures are extensive. In particular, meta-structures can be very useful for improving (ultra-lightweighting) components that have strict surface conforming constraints, such as aerodynamic or fluid-interacting structures, where the surface is proscribed by flow requirements, and components that have multiple complex fixed-flexible connections.
Watch the short ~1 minute video tech demos (links below) for both of these HGon structures: - Video tech demo for single connection HGon: Youtube link. - Full video tech demo for 3-Connection HGon: Youtube link. In Part 3, I'll describe how the HGon meta-structure joints and struts can be subdivided, enabling multi-component and multi-material and multi-domain generation and optimization strategies. Imagine this: the joints can be printed in a rubber-like material, while the struts are stiff nylon or metal tubes (off the shelf), or vice-versa! With segmented HGons, you only have to print the joints... this enables the potential for large, even architectural scale meta-structures... I'll show some examples in Part 3. Thanks for reading, and as always your comments and questions are very welcome. Please email me, or register on our contact page for further info (nothing shared, no lists, no spam ever).
1 Comment
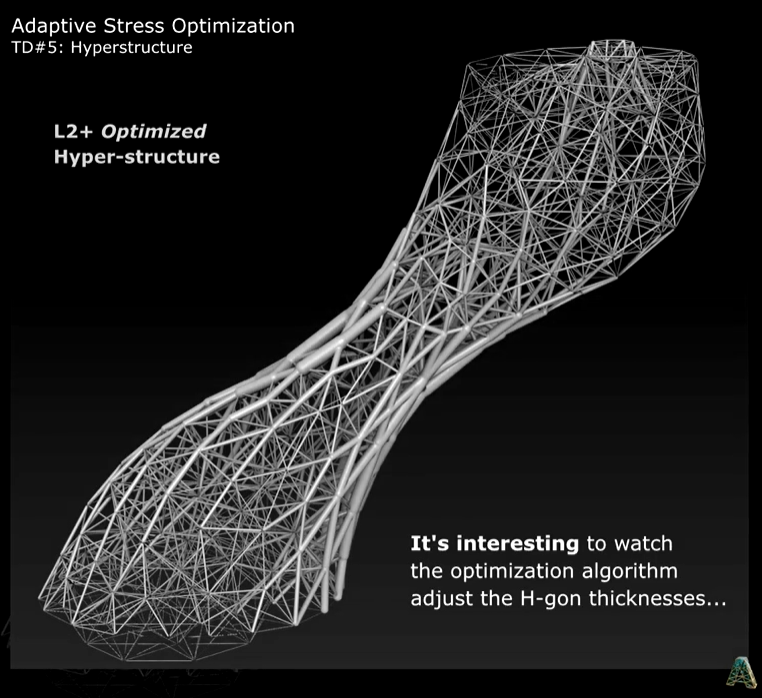
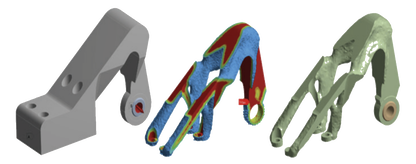
We soon discovered that HGon meta-structures (we call them hyper-gons, or HGons™ for short) have remarkable capabilities for extreme ultra-lightweighting, antivibration properties, and the ability to conform to very complex shapes in ways not possible with lattices. Our initial (and continuing) application was anti-vibration components for novel robotic microscopy systems. Since then we've worked on applications in Aerospace, Automotive, Bio-engineering, Footwear, Architecture/Design, Nuclear, and many others. For further reading, I've written a more detailed history of HGons (meshagons) on my personal webpage: see The Brief Story, development of Meshagons and Hyper-Structures. Meta-topology optimization vs. surface optimization (very brief) With standard topology optimization, the basic procedure is to change the surface of the component to reduce mass or other property. This surface change is usually driven by some stress-based calculation, but the main point is that the optimization only affects the surface. There are many software tools available for this process. Below is an example from ANSYS: Surface-based topology optimization (SBTO) is great for mass reduction and removing 'unstressed' regions of a component, however it is restricted to a single enclosing surface. With meta-structure topology optimization (MSTO), we add the capability for optimization of the internal structures. Outer surfaces can either be held constrained, or also allowed to vary according to stress calculations. This opens up a whole new world of options. For instance, local density and strut-joint thickness (strength) can be controlled and adapted in ways never before possible. The short video clip below shows a simple example for an automotive wishbone component. NOTE how the meta-struts are 'thickened' where computed (FEA) stress is highest, and thinned (or removed) where stress is low. This new type of meta-optimization enables components to be extremely lightweighted and strong - internally adapted/optimized to the surface boundary and loading conditions. Using Meta-optimization (MSTO), the meta-component is over %60 lighter, and %35 stronger -- and this is just a simple 1st step optimization. Multiple iterative strategies and loading conditions can be used such as dynamic/vibration and fatigue calculations. Combining SBTW and MTSO is also a fascinating concept we are working on that dramatically expands the solution space for topological optimization strategies.
In Part 2 I'll show some examples of meta-parametric strategies for optimization and new capabilities for conforming to highly complex structures and connecting surfaces. Thanks for reading, and any feedback or comments/question are surely welcome. Intro: Hello friends, Welcome to the HYPER-BLOG where I'll be posting interesting things I discover (and we develop) about Meta-structures, complex shape generation, and all kinds of always super-interesting related info :) I'll be describing some of our innovations and achievements here at ABĒMIS, and also info that I get from colleagues and around the internet wilderness. In the last 5 years or so (umm, I guess maybe 10 years now) I've been working intensely on developing and generating a new type of meta-structure for ultra-light components. Not lattices, but hyper-structures. True, iterative, and now fractal meta-structures. Here is a super-short 1-min, now ancient :) introduction: Youtube link One of our newer demo-reels with more complex shapes: Youtube link And a bit longer 2.5-min introduction: Youtube link Along the way, I've learned a great deal with the help of the online community and colleagues all over the world... I'll be sharing some of that here. Many thanks to all, and I will always credit external content in all posts. Comments are always welcome, Let's keep it civil and scientific-ish. Hope you enjoy! T.C. Doehring CEO, ABĒMIS llc [email protected] |
by T.C.DOE (CEO)T.C. Doehring: Bioengineer (PhD) and now intensely interested in meta-structures and Additive Manufacturing. I'm a programmer, 3D modeler, and just hack math-person... ARCHIVESCATEGORIES |
Patents awarded 2022-24 (US10585420B2). New 6/2024, AI patents are filed/accepted.
Phone: +1-215-948-2363
Page updated: 7/2024. All info, images, and video Copyright Abemis llc, 2024
Phone: +1-215-948-2363
Page updated: 7/2024. All info, images, and video Copyright Abemis llc, 2024







 RSS Feed
RSS Feed